There are several methods through which height/elevation can be measured using satellite image and aerial photographs. In case of satellite image such as, Cartosat, ASTER, Worldview I & II and others are used to create height or elevation data in the form of digital elevation model.
Aerial photography, LiDAR mapping are very common for creation of elevation data on higher scale/resolution for detailed study.
In the last article, relief displacement used to measure height of any object on earth surface. Here in this another method will be discussed to measure height of any given object on the earth surface.
Parallax for Height Measurement using Aerial Photography
Parallax Concept
Photogrammetry is capable of measuring elevation of earth surface. Aerial photographs/stereo pair satellite images can be used to measure elevation differences through the use of parallax method.
New launched satellite are providing stereo pair satellite images images such worldview-2 etc.
Parallax can be defined as the apparent displacement of a point due to a change in view of the point.
One of the parallax example for human eye can be explained by a simple exercise of childhood.
i.e. hold finger in front of eyes and look at finger, where it is relative to a wall in the background with your right eye. Then look at it with your left eye and its appearance relative to the wall has changed.
This relative change in appearance is due to parallax. It took place due to change in view point for the finger.
Parallax of Aerial Photographs
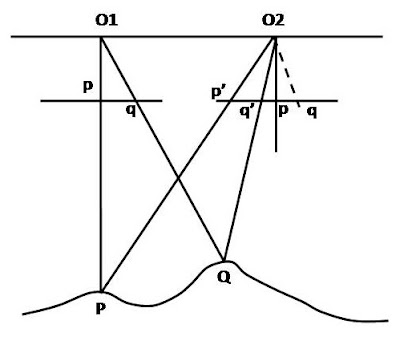
Parallax can be described by below figure
In this figure point P & Q on surface are captured on two aerial photographs as p & q respectively.
- Consider that at one instant the airplane is at O1, vertically above a point P. The image of P will appear at p on the image plane.
- After sometime when the plane is at O2, P will appear as p‘ on this image plane. The ground point P appear as p on first image plane and p’ on the second image plane so this shift of pp‘ in the position of the image of P on the image plane is the parallax of P.
- Similarly for any other point Q, one instant the airplane is at O1, vertically above a point P. The image of Q will appear at q on the image plane.
- After sometime when the plane is at O2, Q will appear as q’ on this image plane. The ground point Q appear as q on first image plane and q’ on the second image plane so this shift of qq‘ in the position of the image of Q on the image plane is the parallax of Q.
Types of Parallax for Aerial Photographs
There are two types of Parallax;Absolute Parallax and Differential Parallax
Absolute Parallax (X-Parallax/Horizontal Parallax): This parallax is in the X direction, It is the algebraic difference of the distances of the two images from their respective photograph nadirs, measured in horizontal plane and parallel to the airbase.
Differential Parallax(Y-Parallax): This parallax in Y direction, the difference between the perpendicular distance of two the images of a point from the vertical plane containing the airbase.
Y-parallax is an indication of tilt in either or both photographs, or a difference in a flying height.
Parallax used for height determination by below method
∆p H’
∆h = ———–
pc
∆h = ha – hc
where
∆h = change in elevation between two points a and c
∆p = parallax of point a subtracted from parallax of point c
H’ = flying height of airplane
pc = parallax of point c
while measuring height using Parallax, below are required
- Any point being measured has to appear on both aerial photos that overlap
- If elevation (benchmark) of point c has known and then its parallax can be measured
- Any point a’s elevation can be calculated relative to point c’s known elevation
- Parallax measurement facilitates computation of an elevation model of ground using aerial photographs.
Numerical Example
Question. Benchmark c has an elevation of 1545.32 ft., x coordinate on left photo of +74.12 mm and on right photo of -18.41 mm. Unknown point a has x coordinate on left photo of +65.78 mm and on right photo of -24.38 mm. If flying height above average ground is 3000 ft. what is the elevation of point a?
Solution. Parallax is the change in x coordinates defined as parallel to the flight line.
Parallax of point c = 74.12 – (-18.41) = 92.53 mm
Parallax of point a = 65.78 – (-24.38) = 90.16 mm
Height measured using below formula
∆p H’
∆h = ha – hc = ———–
pc
here all values calculated below
∆p = pa – pc = 90.16 – 92.53 = -2.37 mm
∆h = (-2.37 mm) * (3000 ft.) / 92.53 mm
∆h = -76.84 ft.
By putting ∆h value in below equation
ha = hc + ∆h = 1545.32 + (-76.84)
ha= 1468.48 ft.
It can be assumed from question that if point a has less parallax so it should have lower elevation than point c.
This Parallax concept is important in aerial photography as this can be used to measure the height of ground.
Childhood exercise example was really good, keep the good work up Sir, really appreciate.
I am really happy to say it’s an interesting post to read . I learn new information from your article , you are doing a great job.Dubai Drone Videography
such a nice piece of article. Thank you for sharing your knowledge. This is a very valuable thing you shared. good stuff!!Professional Photographer Indonesia
In The Heights Full Movie Free Download Watch Online Moviesflix
Best and Famous Rockfon Industrial Products in Australia
Sir, Please explain on importance of parallax in photogrammetry
Thanks for choose Perth Family Photographer, Its very nice for your all fuctions.
Why is that they are subtracting parallax of c from that of a to get a negative answer
And why from the formula of finding Dh ,, we divide by pc and not pa
We will provide you with a team of high qualified tax accountants with an exceptional reputation and the authority to deliver strategic tax advisors near me